Almost flat manifold

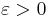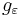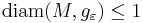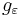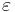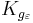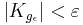In mathematics, a smooth compact manifold M is called almost flat if for any $\varepsilon>0$ there is a Riemannian metric $g_\varepsilon$ on M such that $\mbox{diam}(M,g_\varepsilon)\le 1$ and $g_\varepsilon$ is $\varepsilon$ -flat, i.e. for sectional curvature of $K_{g_\varepsilon}$ we have $|K_{g_\epsilon}| < \varepsilon$ .

In fact, given n, there is a positive number 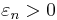$\varepsilon_n>0$ such that if a n-dimensional manifold admits an 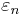$\varepsilon_n$ -flat metric with diameter 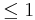$\le 1$ then it is almost flat. On the other hand you can fix the bound of sectional curvature and finally you get the diameter going to zero, so the almost flat manifold is a special case of a collapsing manifold, which is collapsing along all directions.

According to the Gromov—Ruh theorem, M is almost flat if and only if it is infranil. In particular, it is a finite factor of a nilmanifold, which is the total space of a principal torus bundle over a principal torus bundle over a torus.

References

M. Gromov, Almost flat manifolds, J. Differential Geom. 13, 231-241, 1978
E. A. Ruh, Almost flat manifolds, J. Differential Geom. 17, 1-14, 1982